[Deep Learning ] About Neural Networks, 딥러닝 기초개념

출처 : AIT2

 

(8단원 내용 정리)

 

신경망 (Neural Networks)를 학습시키는 방법

Right is better, bcuz 잘 분류하니까 

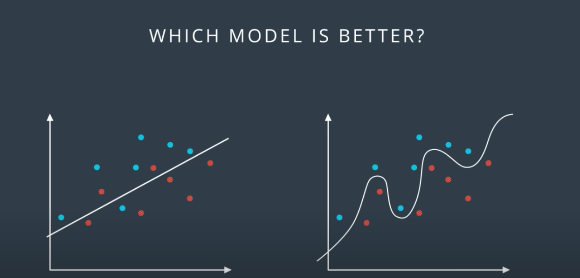
사실상 비선형모델이 학습데이터에 있어서는 지금 오답없이 정확히 두 그룹을 분류하고 있다.

 

Why TESTING?

내부가 하얀 색인 점들은 실전 테스트를 위한 데이터고, 우리는 실전테스트 데이터를 맞추기 위해서 train 데이터를 바탕으로 모델을 학습시킨다. 

 

 

그러나 가끔은 비선형모델 (주로 신경망학습과 같이 복잡한 연산을 바탕으로 정답을 도출하는 모델)이 결코 정답을 잘 맞추리라는 보장은 없는데, 이를 " 과적합 현상"에서 찾을 수 있다.

위 사진에서 보았을 때, 선형모델은 오답이 하나의 점에 불과한 반면, 비선형 모델은 오답인 점이 2개나 발생했다. 이러한 현상은 train 데이터에 너무 과적합된 나머지, 새로운 데이터가 왔을 때 제대로 분류하지 못하기 때문에 발생한다.

 

따라서, 복잡하고 정교하다고 모두 좋은 모델이라 볼 수 없으며, 오히려 간단할수록 좋은 모델일 수도 있다!

 

 

 

Type of Errors, Underfitting and Overfitting

과소적합 (Underfitting)과 과대적합(Overfitting)을 아주 직관적으로 나타낸 설명

과소적합 (Underfitting)과 과대적합(Overfitting)을 아주 적당하게 설명한 예시라고 생각한다. 너무 심각하게 일반화되어서 데이터 전체를 설명할 수 없는 경우 과소적합, 과대적합은 심각하게 학습데이터 위주로 데이터를 설명하는 경우를 의미한다. 감이 안 온다면 다음의 예시를 참고하자.

 

Too Simple? Underfitting.

우선 동물과 동물이 아닌 것을 분류한다고 생각해보자. 위의 예시는 올바르게 동물과 사물을 분리했는가? 아니다. 단순히 개와 개가 아닌 것으로 분류했기 때문에, 고양이는 동물임에도 불구하고 사물로 분류되어 있다. 이렇게 강아지가 아니라는 너무 단순한 이유만으로 일어난 오류를 '과소적합'이라고 부른다. 과소적합인 경우, 노이즈가 많고 bias가 발생해 학습데이터도, 테스트 데이터도 제대로 분류하지 못하는 일이 발생한다. (error due to bias)

 

 

 

TOO Specific? Overfitting. 

보라색 강아지가 왜 잘못 분류되었는가? 이번 예시의 모델은, 강아지를 너무 자세히 묘사해서 분류하고 있다. 학습데이터 내의 모든 강아지의 색상과 같이... 정말로... 자질구레한 특징까지 분류기준으로 삼으니, 테스트 데이터인 보라색 강아지가 등장했을 때에는 제대로 분류하지 못하고 있다.

 

 

좋은 Learning 모델은 자고로,

"A Good Model is like studying well and doing well in the exam."

과적합은 공부라기 보다는 이해도 안하고 교과서 자체를 딸딸 외워서 (물론 한국은 통하겠지만) , 응용문제를 못 푸는 현상과 같음

 

 

Neural Network 내에서 과소적합과 과대적합 

More Generalized, More Correct is the Best.

왼쪽 분류그래프의 경우, 너무 노이즈가 껴있고(학습데이터의 오답률이 높음), 오른쪽은 너무 피팅이 과도하게 된 상태라고 볼 수 있다.

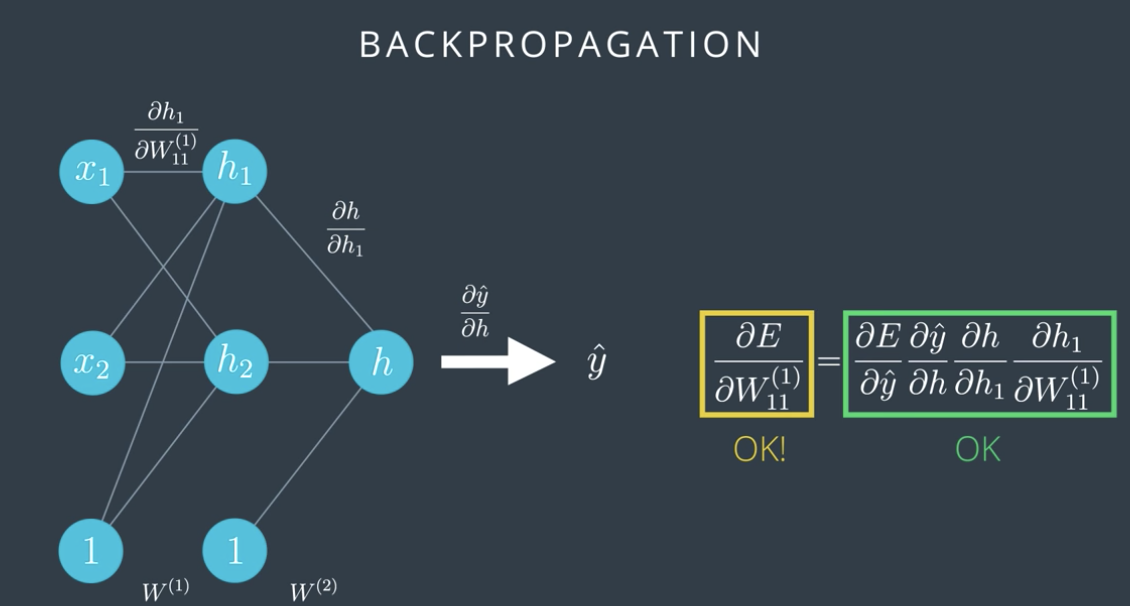
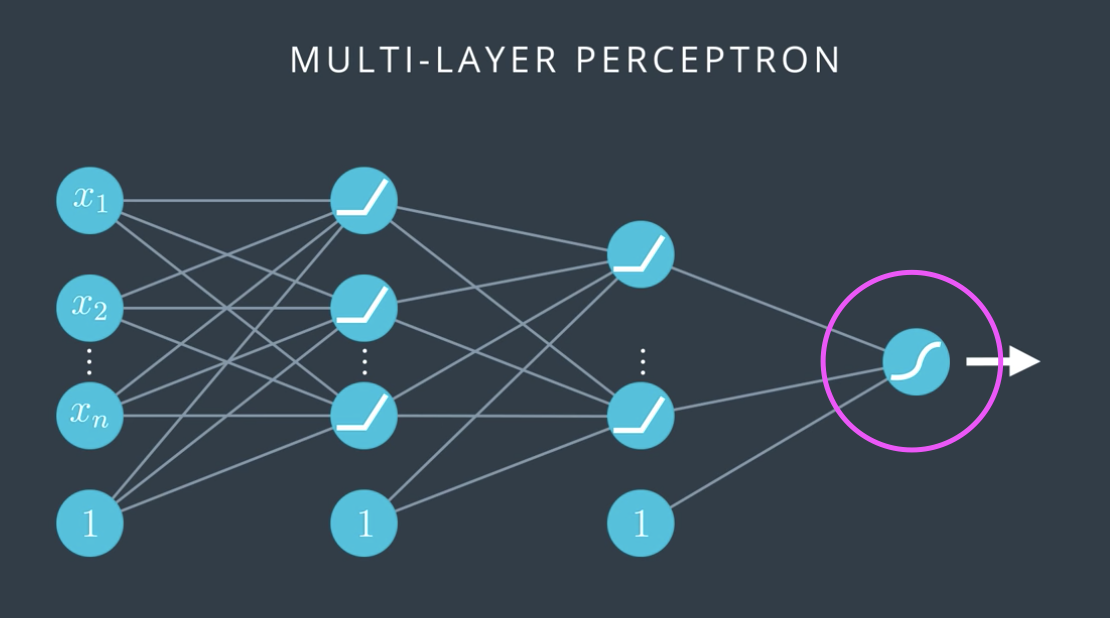
신경망을 도식화 한 그림을 보면, 왼쪽의 경우 신경망층이 매우 적어 현재 선형으로 도출되는 상태를 나타낸다. (just one perceptrons)

반면 오른쪽 그림은, 신경망 층과 가중치가 과도하게 복잡하고 많아서, 과대적합이 된 경우를 보여준다.

 

결국 최적의 신경망 뉴런 수와 은닉층, 노드 수 등을 찾는 일이 가장 중요한데, 이것이 가장 어려운 일이다.

 

지금부터 이를 해결하기 위한 오버피팅을 막을 수 있는 몇 가지 테크닉을 소개하겠다.

(차라리 작은 바지보다는 큰 바지를 사서 벨트를 하자는 주의랄까..)

 

# 학습횟수에 대해 (Epoch)

특히 epoch 600의 경우에는 파란색 점과 아주 가까운 지점에 있음에도 불구하고 빨간색으로 분류할 가능성이 매우 높다...

학습횟수에 따라 Traing, Testing Error를 그래프로 그리면, 학습오류는 학습횟수와 반비례하지만, 테스팅은 오히려 학습량이 과도해지면 높은 오답률을 보이고 있다. 왜 때문이라고? 과적합.

 

 

Model Complexity Graph

• 왼쪽으로 갈수록 Underfitting : High Testing Error, High Training Error 
• 오른쪽으로 갈수록 Underfitting : High Testing Error, Low Training Error 
• 가운데 : Just Right :)

 

결국, Testing Error의  극소점 포인트가 가장 최적의 훈련조건 (여기서는 학습횟수) 이라고 말할 수 있다.

>> ' Early Stopping Algorithm '

 

 

Regulation : Split 2 Points

기계학습에 있어 과적합을 막기 위해서, 예측모델에 어떠한 제약을 주기도 한다.

Using Sigmoid, We could find the Smaller Error model.

두 솔루션 식 중에서 어떤 것이 더 설명력이 좋을까? 어떤 모델이 더 오류가 적을까? 우리가 임의대로 그래프를 그려서는 이 직선이 정확히 분류하고 있는지 알 수 없다.

이제 인공지능 학습에 있어서 뉴런 활성화함수로 쓰이는 'sigmoid' 함수를 대입해서 계산해 본 결과, Solution 2의 경우가 극단적으로 0,1 에 가까운 값을 나타내며 두 점을 명확하게 1,0에 가깝게 분류하고 있다는 점에서, 솔루션 2가 훨씬 괜찮은 분류모델이라고 말할 수 있다. 그러나 일반화 시켰을 때 솔루션2가 더 정답률이 높을까? 정답은 오히려 단순한 모델이 더 나을 수도 있다.

 

 

 

 

가중치에 따라 상이한 결과를 보이는 시그모이드 활성화 함수

왼쪽의 시그모이드는 적절한 경사하강정도를 보이고 있으나 오른쪽 시그모이드 함수는 너무 기울기가 가파르다.

즉, 오른쪽 시그모이드 활성화 함수는 조금만 수치가 바뀌어도 활성화 함수의 결과값이 극단적으로 바뀌고, 이는 오버피팅이나 왜곡된 값(?)을 나타낼 가능성이 크다.

 

그리고 1차식의 최적화를 위해 사용되는 경사하강법(Gradient descent)은 기본적으로 어떤 비선형 함수에서  접선의 기울기가 점점 작아질 때를 최적으로 보고 그 최적점을 찾는데, 우측의 그래프에 접선을 그어보면 아주 기울기가 극적이다(....) (zero and then very large when we get to the middle of the curve)

 

따라서 오른쪽 시그모이드 함수는 매우 certain하고, gradient descent를 적용하기에 여유가 없다. 결국 과적합에 맞춰진 시그모이드 함수는 많은 testing error를 야기한다. 즉, 왼쪽 시그모이드 함수가 일반화된 모델로 사용하기에 더욱 적합하다.

 

 

+) 또한 이러한 기울기의 차이는 가중치 w1, w2에 의해 발생한 것으로 보인다. 나중에 시그모이드함수를 튜닝할 일이 생길 수 있으니 체크.

 

 

참고 : Gradient Descent에 대한 설명

https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95

경사 하강법 - 위키백과, 우리 모두의 백과사전

 

 

 

 

과대적합 솔루션 : Regulation 부여해서 예측모델 계산하는 방법

 

과적합을 피하기 위해 일종의 제약식을 걸어준다 : Regulation

1. 높은 coefficient (w) 에 패널티를 부과한다.

2. Error Function 튜닝 : weights ( = coefficient = w)가 높은 경우에 더욱 큰 값이 나오도록 기존 error function에 람다 이하를 더해준다.

 

여기서 람다식을 어떻게 표현하느냐에 따라서 L1, L2로 규제식이 나뉜다. L1은 weights의 절대값 합을 더하는 반면에 L2는 weights의 제곱합을 더한다는 차이가 있지만, weights가 커지면 람다이하도 커진다는 점은 동일하다. 람다는 우리(사용자)가 weights에 페널티를 부과하는 정도를 나타내는 파라미터다.

 

 

L1, L2 Regulation 비교

L1 규제 

feature selection이 목적이라면 적합한 모델.

그러나 L1 규제를 적용시켰을 때, 0,1로 구성된, 그리고 0이 대부분인 "희소행렬" 골로 도 아웃풋이 도출된다.

Small weights 는 아예 0이 되는 경향이 있다.

weights 의 수를 줄이고 싶거나, small set 으로 만들고 싶을 때 사용 : 약간 PCA 처럼 고차원의, feature가 많은 데이터를 명료하게 만들기 위해 사용

 

 

 

L2규제 

어떤 피쳐를 0이나 1같이 극단적인 값으로 보내기 보다는, 모든 weights를 동질적으로 작은 규모로 유지시키는데 초점

대부분의 training models에 적합.

 

 

Why would L1 regularization produce vectors with sparse weights, and L2 regualtion will produce vectors with small homogeneous weights?

 

- (0,1)이든 (0.5, 0,5)든 총 weights의 합 1

- 그러나 (0.5, 0.5)의 경우 L2처럼 제곱합을 하면, 결국 0.5 도출

- 따라서 L2는 (0.5, 0.5)에 대해서 더 작은 제곱합을 제공해주므로 (0.5, 0.5)를 더 선호

 

 

 

DropOut

아까 언급한 바대로, 신경망 내에 너무 많은 노드와 은닉층이 있으면 그만큼 과적합될 가능성이 높아진다. 따라서, 임의로 몇 개의 노드를 랜덤으로 끄고 학습을 시켜 과도하게 모델이 학습되는 것을 막는다. dropout=0.1 이면, 전체 노드 중 10%를 임의로 끄고 모델 학습을 한다는 뜻.

 

 

 

 

 

 

 

 

Gradient Descent : To find the Global Mininum, we restart randomly.

 

 

 

 

 

Vanishing Descent of Sigmoid Function 

시그모이드 함수의 경우 공역이 [0, 1]의 범위 내에서 정의 되며, 양 옆 극단으로 갈수록 derivatives가 0에 수렴하는 현상을 보인다. 그런데 derivatives는 앞으로 어느 방향으로 연산이 나아갈지를 정하는 중요한 파라미터(?)로, 양 극단이 0이 되어버리면 그 방향성을 잡는데 큰 어려움이 생긴다. 이는 선형 퍼셉트론에서 문제가 더욱 심각해지는 데 다음의 그림을 참고하자

 

 

 

 

 

해결책 : Change the Activate Function

 

 

 

 

 

 

 

 

 

Relu can improve the training significantly without sacrificing much accuracy, since the derivative is one if the number is positive.
It's fascinating that this function which barely breaks linearity can lead to such complex non-linear solutions.

 

 

 

 

 

 

 

 

Batch vs Stochastic Gradient Descent

Number of Steps = Epochs 

 

 

 

 

Well, here's a question : Do we need to plug in all our data every time we take a step?

일부 작은 데이터만을 가지고 학습시키면 확실히 빠르고, 만약 데이터가 well-distributed하다면 좋은 결과를 낼 수 있다. --> SDG를 사용하는 배경! 

 

Stochastic Gradient Descent (SGD)

https://blog.naver.com/ehdrndd/221784254473

Stochastic Gradient Descent(SGD)

내가 공부하고 있는 AIT 보다는 위의 블로그가 더 명확하고 이해하기 쉽게 설명하고 있는 것 같아 첨부.

 

배치방식의 경사하강법은 데이터 전체를 학습시켜서 파라미터를 변경하는 방식이라면, SDG는 차라리 파라미터를 300만번 바꾸자. (그러니까 데이터 하나 당 매번 파라미터를 바꾸는 방식)라는 개념이다. 확실히 전자가 연산 수가 적긴 하지만, 지그재그로 파라미터가 움직이기 때문에 정확한 Local Minimum 값을 찾기는 힘들다. 그래도 확실히 속도가 빠르다는 점에서 강점.

 

배치방식은 전체 데이터를 몇 개의 묶음 (batch)로 나누어 학습을 시키는 방식. 그럼에도 불구하고 여러 개의 데이터를 학습시킨 후 파라미터를 업그레이드 하기 때문에 속도에 영향이 있는 것으로 보인다.

 

Local Minumum 문제 해결 1 : Learning Rate

만약 너무 Learning Rate가 크면 step이 너무 커서 정확한 minimum 포인트를 찾을 수 없게 되어 chaotic 해진다.

따라서 Learnign Rate는 적당히 작을수록 Global minimum에 정상적으로 도달할 가능성이 더 높아진다.

 

 

To find the best "Decreasing Learning Rate"

• If Steep : Long Step
• If Plain : Small Step

 

Local Minimum 문제해결2  : Momentum

Momentum of Derivatives

시계열 분석 방법에서 이동평균법과 비슷한 개념처럼, 최근의 데이터에 더 가중치를 많이 주면서 스텝 간격을 조정하면,

유의하지 않은 변곡점 포인트는 무시하고 유의한 변곡점 포인트에 가까워 질수록 small step으로 지나갈 수 있도록 하여 최적의 오류 극소점을 찾는 방법. 학습률을 조정하는 방법은 전체적인 스텝을 조정하는 방식이였다면, 모멘텀 방법은 최적의 극소점이 나타나기 전까지 스텝을 조정하면서 효율적으로 목표에 도달하는 방법.